Overwhelmed by the huge number of custom operators in Haskell? Work with a popular library, but it looks overly intimidating due to the abundance of intricate-looking operators? For many Haskell engineers, these problems are real. Developers can experience massive anxiety, based solely on the fact that they need to deal with such API that throws a bunch of custom operators in their faces (we call such interfaces “inthefaces”).

To get a deeper understanding of the problem and develop firefighting techniques, let’s have a closer look at operators and how to work with them.

This post is useful for both newcomers and language adepts, seeking ground rules around using operators and must-do things when introducing your own operators.

Difficulty🔗

Let’s first discuss why custom operators often feel so unfriendly. Since Haskell allows defining custom operators, you can find many creative symbolic names used for diverse purposes in various codebases. Unfortunately, they can decrease readability and maintainability and increase the entrance threshold for new joiners.

When you see an unfamiliar operator (e.g. %~|), usually it’s not clear what it should do solely from its name. If you are familiar with some guidance of operator naming in a particular context, you could figure out the meaning by analysing each symbol. But in general, there are no rules; you’re on your own.

The arbitrary-looking name doesn’t provide any hint to guide you through code understanding when you see it for the first time. Moreover, even if you manage to get the logic of custom operators, this information vanishes out of your brain the second after you finish using it. In other words, such knowledge is not long-term unless you use it all the time (e.g. +, /=, etc.).

Unfortunately, another difficulty point of operators is that they bring an additional layer of complexity — implicit parentheses. The compiler has special rules for parsing expressions with operators (unlike ordinary functions), determined by each operator independently. The compilation result, driven by individual rules for every operator, sets your code’s correctness and even performance: you may see unexpected compiler errors (inability to parse expression) or even wrong runtime results when mixing different operators.

However, despite all challenges associated with using operators, careful usage can lead to elegant and idiomatic solutions. This is crucial when you are creating embedded domain-specific languages (eDSL). So it is absolutely necessary knowledge to have in your pocket.

Definitions🔗

As a guide through the dark forest of operators and brackets, this blog post focuses on operator fixity — a Haskell feature controlling the associativity and precedence of operators (explained later). Fixity glues different operators and controls their behaviour. When used properly, this feature helps to write more maintainable code and provide more convenient APIs.

Before we proceed further and dive into the main fixity part, let’s walk through the basic definitions we need in order to work with operators.

Even though operators may seem straightforward, in reality, it’s a convoluted topic that involves multiple different concepts:

• Operator
• Notation
• Arity
• Associativity
• Precedence

To understand how operators are used, we will go through the definition of each concept with explanation and examples.

Operator🔗

The below table contains a few standard operators in Haskell:

According to the Haskell 2010 Report, only the following characters are allowed to be used as operator symbols:

! $ % & ⋆ + . / < = > ? @ \ ^ | - ~ : #

However, not all variants of these symbols are possible to use as operators. The following combinations are already reserved for built-ins and syntax, so you can’t define your custom operators using the exact names from the list below:

• .. — list range syntax for enumerations
• : — list constructor (operator for prepending elements to lists)
• :: — type signature
• = — defining functions, data types and variables
• \ — escaping characters and multiline strings gaps
• | — alternatives: guards and constructors in sum types
• <- and -> — function arrows, binding variables, and much more; check our separate blog post to explore the entire Arrows Zoo
• @ — as-patterns and visible type applications
• ~ — irrefutable patterns
• => — contexts (aka constraints) in functions and instances

Arity🔗

All functions can have zero to many input elements and only one output. So, if we have + that takes two numbers and returns the result of their addition, then we can say that the arity of + is equal to two.

The following terms represent the most common arities:

• Nullary — zero arguments
• Unary — single argument
• Binary — two arguments
• Ternary — three arguments

This guide focuses on binary operators as they are the most common in the ecosystem. However, keep in mind that operators of other arities can perfectly exist as well.

Nullary operators*🔗

You can go one step further with improving your eDSLs in Haskell and define a nullary operator (an operator that takes no arguments). This feature doesn’t require any language extensions.

For example, we use it in Stan to define more readable AST patterns that match specific Haskell code :

(?) :: PatternAst
(?) = PatternAstAnything

Note that when using the nullary operator, you need to put it in parentheses:

opApp (httpLit ||| urlName) addPathOp (?)
|||
opApp (?) addPathOp urlName

Notation🔗

By default, operators are used in the infix form. Here is an example of multiplying two numbers using a binary operator *:

24 * 16

You can see that this is indeed the infix form, as * itself is positioned between two input numbers.

Every operator could additionally be transformed into prefix form. To use an operator in the prefix form, put it in () and move its position to the first place (like for ordinary functions):

(*) 24 16

Unlike operators, ordinary functions by default are used in the prefix form. For instance, below is an example of a binary function elem, used in its prefix form and supplied with two arguments:

elem 5 myList

However, you can use a function in the infix form as well! For that, you need to put it in backticks (```) and change its position:

5 `elem` myList

In sum, you actually have four ways to use one function/operator (as they often come together).

plus 3 4     -- function in prefix form (default)
3 `plus` 4   -- function in infix form
3 + 4        -- operator in infix form (default)
(+) 3 4      -- operator in prefix form

The most interesting notation that we are going to focus on is the infix form of operators and functions. The compiler treats them differently from prefix ones, and they also come with a special mechanism controlling their behaviour which we look into in further steps.

Postfix operators*🔗

To use this feature, you need to enable the PostfixOperators language extension. However, you need to put your operator application (operator together with its argument) in parentheses.

The most popular example of using this feature is writing a fancy factorial:

{-# LANGUAGE PostfixOperators #-}

(!) :: Integer -> Integer
(!) n = product [1..n]

ghci> (10!)
3628800

Another example of using postfix operators is the improvement of the eDSL for the Haskell CSS library clay by allowing to write size in percentages:

(%) :: Rational -> Size Percentage
(%) = fromRational

css :: Css
css = do
    footer <> header ? do
        width (100%)
        maxWidth (100%)
        backgroundColor lightGrey

    footer ? marginTop (2%)

Associativity🔗

Let’s look at an example to understand better what associativity means. If you have a binary operator ◯ and you write the following expression:

a ◯ b ◯ c ◯ d

There are several ways how () can be placed:

1. ((a ◯ b) ◯ c) ◯ d
2. a ◯ (b ◯ (c ◯ d))
3. (a ◯ b) ◯ (c ◯ d)
4. a ◯ ((b ◯ c) ◯ d)
5. (a ◯ (b ◯ c)) ◯ d

Other ways of placing () – options 3-5 – don’t have names, and usually brackets are not placed in such ways automatically. Such combinations can be achieved only through manual placement.

The exact definition explained with a formula:

a ◯ b ◯ c ≡ a ◯ (b ◯ c) ≡ (a ◯ b) ◯ c

Some common examples of associative operators include addition, multiplication, list appending, function composition, function application, boolean “and”, boolean “or”.

On the other hand, operators such as subtraction, division, equality, comparison don’t satisfy this property.

The consequence of the operator being associative is that it doesn’t matter how you place (); the result will always be the same. So, if placing parentheses can affect the performance, you can set them differently and still get the same result but faster.

👩‍🔬 The associativity property becomes crucial in some cases. The <> (append) operator from the Semigroup typeclass must be associative for a lawful Semigroup instance. Abiding the associativity law makes code correct because other functions rely on sane behaviour described by the typeclass law.

For example, the stimes function implements appending the same value to itself n times. It uses the benefits of associativity for a more performant implementation that runs in O(log n) time instead of naive O(n). If an instance violates Semigroup laws, this efficient default implementation of stimes produces invalid results.

For example, the operator of the integer comparison can’t be used several times:

-- ❌ incorrect
1 <= x <= 10

Indeed, it would be nice to be able to write the code above to describe concise range checks. However, it’s not possible, and you need to write it like this:

-- ✅ correct
1 <= x && x <= 10

One way to understand the reason for this is to look at types:

(<=) :: Int -> Int -> Bool

You can see that a specialised version of the <= operator takes two Ints and returns a Bool, so it can’t be chained because the return type can’t be matched with the input type. However, this is not universally true for all operators with different input and output types. Polymorphic operators still can have associativity and be chained.

Precedence🔗

While associativity is a handy property when dealing with the series of one operator usages, it wouldn’t answer the question “which operator to apply first if I deal with several in a single expression?” It makes the following known “puzzle” so tricky without diligent thinking:

2 + 2 * 4

Therefore, it’s not enough to know their associativity to figure out how () will be placed when using different operators. You also need to have information about their precedence.

For example, we know that * has higher precedence than + from school math classes. Thus, when we write 2 + 3 * 4, we understand this expression as 2 + (3 * 4) and not (2 + 3) * 4. Therefore, we conclude that * has higher priority over +.

But what happens if you use school operators in a programming language? The compiler didn’t go to school; hence it doesn’t know about these conventions. And that’s why it needs some ground rules about their priorities.

Even if you embed rules for several common operators directly in the compiler, you won’t get the same level of control for custom operators from some external libraries. How will the compiler know a proper way to place the brackets? It won’t. No standard rules are telling how the compiler should behave based exclusively on operator names. The priority information is specific to each use case and needs to be learned.

abs n `mod` 100 `div` 10

((abs n) `mod` 100) `div` 10

If you want to check the placement of brackets in a Haskell expression quickly, you can use the following TemplateHaskell trick in GHCi by putting your expression inside $([| |]).

$ ghci -ddump-splices -XTemplateHaskell
ghci> $([| readMaybe <$> getLine >>= print |])
<interactive>:1:3-39: Splicing expression
    [| readMaybe <$> getLine >>= print |]
  ======>
    ((readMaybe <$> getLine) >>= print)

👩‍🔬 In the above code, we use the quotation brackets [| ... |] to parse an expression into Haskell AST using the GHC parser. Then we convert it back to Haskell using the Template Haskell splice $(...). This invokes the TemplateHaskell pretty-printer that inserts all implicit parentheses for us.

The key part of the above output is the last line: ((readMaybe <$> getLine) >>= print). Here we can see how the compiler consumes this expression and puts the brackets for us. From this example, we can say that <$> operation will be applied first, and only then the bind operator >>= will use the result. That means that <$> has higher priority than >>=.

As we finished with all the necessary terms and concepts, let’s move to the following section, where we are going to learn how to use (and specify) all this information for your own operators.

Fixity declaration🔗

Previously we saw that the compiler uses information about operators associativity and precedence to parse expressions correctly. However, this algorithm is not magical, and information about standard operators is not hard-coded in the compiler internals.

In Haskell, all operations have this information without any exceptions. To manually specify operator associativity and precedence, you can use syntax called fixity declaration.

And, consequently, all standard operators have fixity declarations too. In fact, the Haskell 2010 Report specifies associativity and precedence for operators from the standard library base.

In order to define the fixity for your operator, you need to write a special declaration in the same module as your defined function. The general shape of a fixity declaration is the following:

infix[l|r] NUMBER <Comma-separated operators>

Explanation of the above syntax:

• The first keyword defines associativity:
  • infix — non-associative
  • infixr — right-associative
  • infixl — left-associative
• The NUMBER defines operator precedence. It must be in the range between 0 and 9 inclusive. The higher number implies higher precedence.
• Then, you enumerate a comma-separated list of operators that would have declared associativity and precedence.

⚠️ If you don’t specify fixity for an operator, it will use the default, which is infixl 9

ℹ️ There was a GHC proposal to allow a more flexible scheme for the operator precedence, but the proposal was closed.

• GHC proposal: Use nontotal precedence for operators

The below image summarises the relation between Haskell syntax and operator associativity:

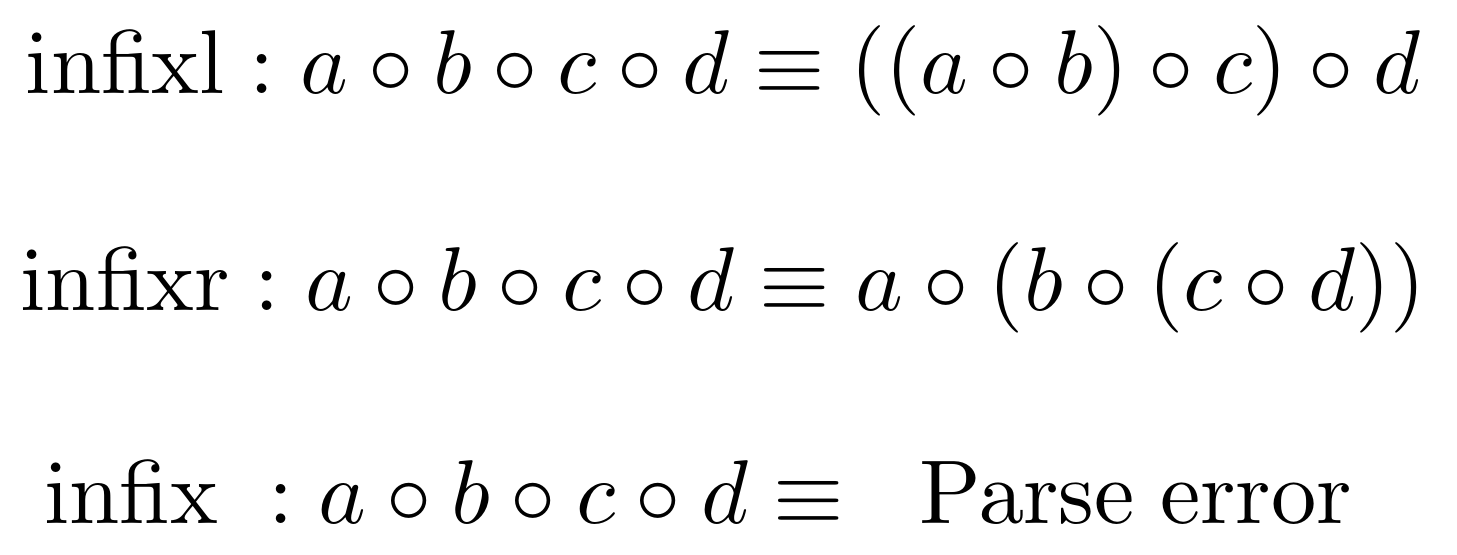
Fun part*🔗

The following real-life analogies of operator associativity can help with remembering the rules around placing brackets:

• When a dog eats food, it eats immediately everything that is given to it. So a dog eating food is infixl.

• When you try to feed a cat, it first needs to sniff (evaluate) all provided food and only then it can start eating it. So a cat eating food is infixr.

• When you pet a parrot, it bytes the first piece but most of the food goes past it right on the floor. That’s why a parrot eating food is infix.

The following type signatures demonstrate the above analogies:

🥣 :: 🐕 -> 🥩 -> 🐕
🍽 :: 🐠 -> 🐈 -> 🐈
🎯 :: 🦜 -> 🌽 -> 🐥

Applying the same operator multiple times helps to recall its associativity:

🥣(🥣(🥣🐕🥩)🥩)🥩
🍽🐠(🍽🐠(🍽🐠🐈))
🎯🦜🌽

For better performance, infixl operators should be eager (just like dogs). And infixr operators in Haskell are usually lazy (similar to cats). And, of course, infix operators are wild.

Standard examples🔗

Now, let’s see a few examples from the standard library. Here are a few common operators as they are defined in base:

-- operator fixities for comparison operators
infix  4  ==, /=, <, <=, >=, >

-- | Boolean "and" operator.
infixr 3  &&
(&&) :: Bool -> Bool -> Bool

-- | Boolean "or" operator.
infixr 2  ||
(||) :: Bool -> Bool -> Bool

infixl 4 <$>
(<$>) :: Functor f => (a -> b) -> f a -> f b
(<$>) = fmap

The above examples are suggesting us that the following information is held:

• Comparison operators (e.g. ==, <) are non-associative.
• Boolean “and” (&&) and “or” (||) operators are right-associative, so the expression x && y && z parses as x && (y && z). This is important because those operators are lazy in their second (right) argument.
• Operator && has higher precedence than ||, so the expression x && y || z parses as (x && y) || z.
• Comparison operators have higher precedence than boolean operators, so you don’t need to use () around comparisons when performing multiple checks:
  • isBetween (a, b) x = a <= x && x <= b
  • outOfBounds (a, b) x = a <= b && (x < a || b < x)
• The functor operator <$> is left-associative, meaning that f <$> g <$> x parses as (f <$> g) <$> x, but it still works anyway because the Functor instance for a function is a function composition. So the previous expression is equal to f . g <$> x but you may see slightly worse error messages in case of errors when using multiple functor operators instead of the composition.

infixr 1 ==>
(==>) :: Bool -> Bool -> Bool
a ==> b = not a || b

ghci> False ==> False ==> False

ghci> False ==> (False ==> False)

ghci> (False ==> False) ==> False

ghci> True || True  ==> False

ghci> (True || True)  ==> False

ghci> True || (True ==> False)

ghci> False ==> False ==> False
True
ghci> False ==> (False ==> False)
True
ghci> (False ==> False) ==> False
False
ghci> True || True  ==> False
False
ghci> (True || True)  ==> False
False
ghci> True || (True ==> False)
True

Discovering fixity🔗

Though fixity is critical information for writing correct and performant code, fixity is only visible on the declaration level, but not during the usage. However, there are ways to find it out for yourself.

You can get the information about the fixity using the :i command in GHCi. The command gives not only the type signature, module it is coming from but also data about fixity.

ghci> :i (&&)
(&&) :: Bool -> Bool -> Bool 	-- Defined in 'GHC.Classes'
infixr 3 &&

Another way to discover fixity is to check the documentation. Haddock renders fixity information near the type signature, so you can also see it when browsing through the docs:

⚠️ Currently, you will see the fixity information only if the operator has an explicit fixity declaration. If the implicit default one is used (infixl 9), neither Haddock nor GHCi displays it.

Functions fixity🔗

We’ve mentioned before that you can turn ordinary functions into operators by using backticks. In that case, the entire operator-specific behaviour applies to them as well, including the ability to specify precedence and associativity via the fixity declaration.

You can write explicit fixity declarations for infix forms of ordinary functions, as shown in the example below. Otherwise, the default fixity infixl 9 will be applied to infix calls of normal functions.

-- | Integer division.
infixl 7 `div`
div :: Integral a => a -> a -> a

-- | Integer modulus.
infixl 7 `mod`
mod :: Integral a => a -> a -> a

Dots on i🔗

The Haskell standard library contains very diverse operators of all forms, shapes and fixities. Let’s look at a few interesting cases of fixity declarations that are extremely useful to know in order to understand how functions work together in the language.

Composition and application are essential parts of Haskell. They are also operators, so let’s look at how they are defined:

-- | Function composition.
infixr 9  .
(.) :: (b -> c) -> (a -> b) -> (a -> c)

-- | Function application.
infixr 0  $
($) :: (a -> b) -> a -> b

The function composition operator has the highest precedence – 9, while the function application operator has the lowest 0.

In other words, function composition will group arguments first, while function application will be applied last. Usually $ is used to avoid redundant (). Compare:

foo list = length (filter odd (map (div 2) (filter even (map (div 7) list))))
foo list = length $ filter odd $ map (div 2) $ filter even $ map (div 7) list

And similarly, it’s common to define functions in Haskell in point-free style using function composition. So the above example can be rewritten using the dot operator:

foo = length . filter odd . map (div 2) . filter even . map (div 7)

Implicit parentheses in the example above resemble the original version:

length . (filter odd . (map (div 2) . (filter even . map (div 7))))

Beyond fixity rules🔗

Even if the lowest precedence that you can give to an operator is 0 and the highest is 9, there are a few special cases where things in Haskell go beyond these rules.

For example, consider the following definition, including function composition:

hasWithLen :: Int -> [[Int]] -> [[Int]]
hasWithLen n = elem n . map (\l -> length l : l)

If you place () explicitly in the function definition, you will get the following expression:

(elem n) . (map (\l -> (length l) : l))

From this, you can see function application (space) has even higher precedence than function composition (.). In some sense, you can think of a space (function application in f x y) as a built-in operator with the highest precedence 10.

Let’s look at another peculiar situation. Even though the Haskell 2010 Report doesn’t specify the fixity for the function arrow, from the code and the GHCi :i command, we observe that the fundamental built-in function arrow has precedence -1:

infixr -1 ->
data (->) a b

Since the arrow is right-associative (as the fixity declaration tells us), we now understand how parentheses are placed in all type signatures and why we can skip them (as we always do) in there.

Int -> (Int -> Bool)  -- same as Int -> Int -> Bool

Another way of looking at this is the following: all functions in Haskell take exactly one argument and return exactly one result. Both the argument and result can be a function. Haskell just provides lots of syntax sugar to make this behaviour invisible on the surface.

Common errors🔗

Using operators can lead to confusing compiler errors in multiple cases due to the fixity conflicts and other tricky moments.

For instance, if you try to use two different operators with the same precedence but different associativity, GHC outputs an error:

ghci> Just 5 == subtract 3 <$> Just 8

<interactive>:7:1: error:
    Precedence parsing error
        cannot mix '==' [infix 4] and '<$>' [infixl 4] in the same infix expression

Or, if you use operator section, applied to the expression that involves multiple operators:

    The operator '<>' [infixr 6] of a section
        must have lower precedence than that of the operand,
          namely '$' [infixr 0]
        in the section: '<> HashSet1.fromList $ x :| xs'

    |
313 |             x:xs -> (<> HashSet1.fromList $ x :| xs)
    |                     ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

Let’s look at another type of errors happening due to the usage of operators. If you want to print a string literal, the simple code works:

putStrLn "The number is 42"

But now you want to print a variable instead of a fixed number, and if you do a straightforward change like below, you will see an error message:

putStrLn "The number is: " ++ show n

    • Couldn't match expected type '[Char]' with actual type 'IO ()'
    • In the first argument of '(++)', namely
        'putStrLn "The number is: "'
      In the expression: putStrLn "The number is: " ++ show n
      In an equation for 'it': it = putStrLn "The number is: " ++ show

The error message tells us that there is a type error, so you might think you’ve probably used a wrong function (either converting to string or appending strings). However, the error, in fact, is due to the precedence of operators. The above expression is parsed by the compiler as follows:

(putStrLn "The number is: ") ++ (show n)

So you’re trying to append the string with the result of printing the string, not with the already written text literal. Now you see that the compiler complains rightfully.

This error can be easily fixed by either using explicit parentheses or using the dollar operator $ (remember its precedence?):

putStrLn ("The number is: " ++ show n)
putStrLn $ "The number is: " ++ show n

Type-level operators🔗

So far, we’ve been discussing only term-level custom operators. However, in Haskell, you also can have type-level operators — types or type-level functions defined using operator symbols. And you can write fixity declarations for them exactly in the same way as for ordinary operators.

Interesting fact: the previous trick with the function arrow’s precedence allows you to define the type-level function application operator similar to the term-level one, and it will work as expected:

infixr 0 $
type family ($) (f :: a -> b) (x :: a) :: b where
    f $ x = f x

foo :: Int -> IO $ Maybe $ Either Int String

We can verify the placement of parentheses in GHCi:

ghci> :t foo
foo :: Int -> IO (Maybe (Either Int String))

Check out the type-operators package for more examples.

Local fixity declarations🔗

Usually, operators are defined globally on the module’s top-level (together with their fixity declarations). However, you can also introduce local variables or even function arguments as operators. And this raises a relevant question: can you define fixities for local operators? The answer is “Yes”.

Haskell allows local fixity declarations — fixity declarations for local variables in let or where. Below is a small example demonstrating this feature:

modSum :: Int -> Int -> Int
modSum x y = x % y + y % x
  where
    infix 7
    (%) :: Int -> Int -> Int
    (%) = mod

In the code above, we define a local operator % as mod (similar to other programming languages), specify a fixity declaration in the same where block, and use it within the function. By providing fixity greater than for the + operator (which is 6), we can omit parentheses and get the correct results as desired.

Similarly, you can define an operator with its fixity declaration using let-in syntax:

operators :: Int -> Int -> Int
operators x y =
    let infixl 8 ^-^
        (^-^) :: Int -> Int -> Int
        a ^-^ b = a ^ 2 - b ^ 2
    in x ^-^ y * y ^-^ x

Moreover, you can even name function arguments as operators during the function declaration. Here is an example of the standard function on that uses this feature:

infixl 0 `on`
on :: (b -> b -> c) -> (a -> b) -> a -> a -> c
(.*.) `on` f = \x y -> f x .*. f y

The function on is defined in infix form using backticks (and it has an associated fixity declaration). It defines its first argument (a binary function) as a variable with the operator name .*.. And then, it uses this operator in the body as an ordinary binary operator.

⚠️ Though, unlike locally defined operators (with let-in and where), you can’t assign fixities to operator arguments using local fixity declarations.

Takeaways🔗

After reading this blog post, you are equipped with the main terminology and functionality around operator usages. Let’s quickly recap the most important highlights:

• Always specify fixities for your operators. Otherwise, the default fixity will be assigned. Better to explicitly say what you want instead of keeping additional overhead about default behaviour in your (and users) mind. Remember also that fixity info is not rendered on Hackage, and even GHCi doesn’t display this information with the :info command when not specified.
• Put operator fixity before the type signature and after Haddock documentation. Our style guide suggests this style. By following it, you will see all the information about the operator in one place.
• Specify associativity even for associative operators. Even if the operation performed by the operator doesn’t care about the order of parentheses, you still need to place () somehow for the operator. Hence, the compiler knows how to evaluate the expression. For instance, the order of () can affect performance in some cases (e.g. for the ++ list appending operator), so keep this in mind when deciding. Usually, functions and operators in Haskell are lazy in their second (right) argument, so infixr is a good default if the operator can be chained. Otherwise, you can use infix. But it’s always better to consult the implementation first and think about potential use-cases before writing the fixity declaration.
• Always use () when different operators are involved. You may see how everything works in trivial cases without explicit brackets. But when expressions become more involved, it may be hard to do so. Additionally, implicit parentheses can unexpectedly result in wrong or misleading outputs. Also, since fixities are user-defined, they may change between versions and lead to unpredictable results. If you’d like to enforce that rule, you can even mark your operator as infix even if it can be associative to force users always to put () explicitly.
• Provide a non-operator version to operators. Using operators can lead to elegant and fancy-looking code, but it’s not necessarily easily maintainable. It is always a good idea to give people a choice of not using operators and rely on more descriptive functions.
• Provide non-unicode versions for Unicode operators. In Haskell, you can define operators using unicode symbols after enabling the UnicodeSyntax extension. But it can be challenging to work with such operators in various scenarios. So don’t sacrifice comfortability in favour of fancy-looking code and definitely provide alternatives.
• Use Stan to detect missing fixity declarations. Haskell static analyser Stan produces a warning when the operator misses fixity declaration.

Careless abuse of operators can lead to less readable code. But knowing operators up and down can help you write code that is both maintainable and elegant. And you can easily say that you’ve mastered operators after reading this comprehensive guide. If you ask us about the one message you can take away from this guide, it would be this:

When defining a lot of custom operators, it makes sense to fixate on fixities. 😉

Links🔗

• Wikipedia: Operator associativity
• Haskell 2010 Report: Fixity Declarations
• GHC User Guide: Local Fixity Declarations
• GHC User Guide: Postfix operators
• GHC User Guide: Unicode Syntax
• Type Classes: Identifiers and operators
• Type Classes: Type Operators
• Quick tip: Postfix operators in GHCi