Along with the popular Functional Programming (FP) concepts such as purity or immutability, there is a significant one, which couldn’t boast much discussion around it — totality. Totality is an exceptionally interesting notion in the FP context. And you probably already use it and are aware of some pitfalls of not having totality in your code, but maybe the terminology doesn’t ring a bell.

In this blog post, we want to provide a comprehensive guide to the concept of totality in Functional Programming by demystifying its meaning, giving a lot of examples, and recommending how to get tools to help you write maintainable, testable code. You will find this blog post helpful if you are interested in understanding the fundamentals of FP.

Note: we will use Haskell to demonstrate and explain the totality, but the involved concepts apply to any programming language.

Ready?

Definition🔗

Functions are core elements of Functional Programming. Functions are expressions that have a type that could be primitive or more complex. We can say that each function has an input, 0 or more arguments of some type and only one output, returning type. In other words, a function transforms its inputs to the output, and the function definition describes what actual work a function does to produce its result.

A function is total if it is defined for all inputs of its corresponding type, or in other words, if a function returns the output on any possible values of the input types.

For example, the following function that checks if the given integer is zero is total:

isZero :: Integer -> Bool
isZero n = n == 0

The above function is defined for any value of type Integer. No matter what it would receive as the argument, it will always return the answer – True or False.

On the other hand, a function like “integral division” is partial (non-total). Though the division works perfectly on most of the inputs, the result of division by zero is not defined; therefore, there is an argument on which the function can’t return a reasonable result (and that’s why you may find the isZero function helpful). Partial functions are not defined on all their inputs and usually blow up when given something they cannot handle.

Is that math?🔗

The definition of totality originated in math. It has a similar formulation to what we provided above and could be understood in the same way.

Total function is a function defined for all elements in its domain. The domain is the set of x-values that can be put into a function. In other words, it’s the set of all possible values of the independent variable.

We can notice that the math function domain is the same as the input of our functions.

The following image is the canonical way to represent math functions, mapping values from domain A to values of range B. If it were a programming function, we would say that it maps type A to type B. Both total and partial way could be illustrated in that manner:

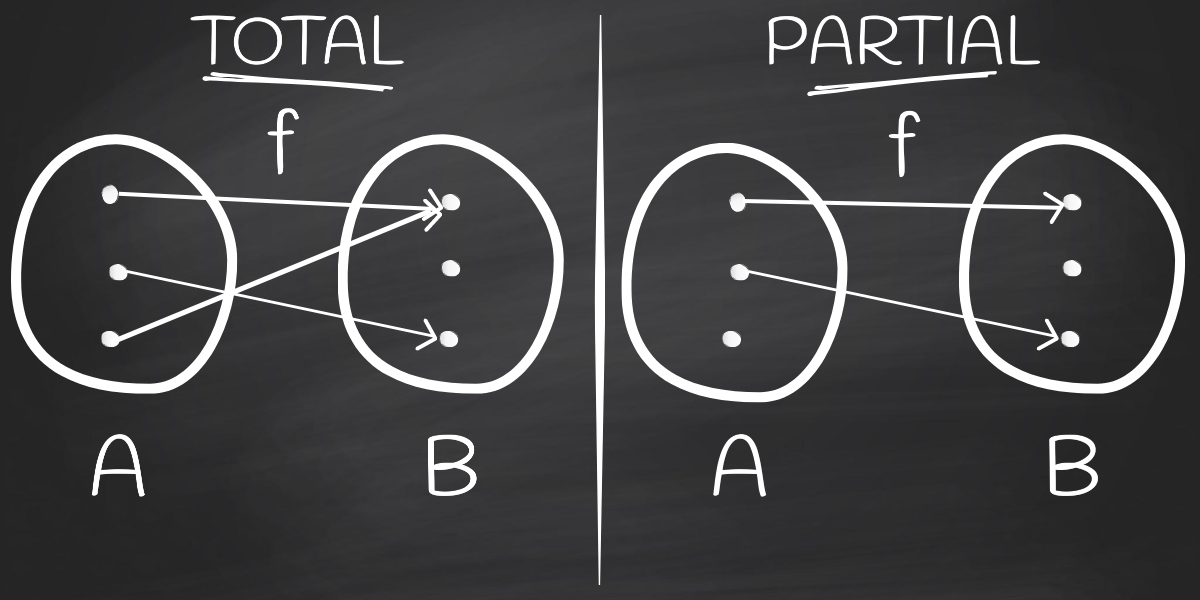
However, despite all similarities, functions in programming are a bit different because they have a notion of computation.

Math doesn’t consider how long it takes for a function to calculate or how much memory it needs. Moreover, functions in programming can hang, and it is vital to keep this in mind when you write code.

Functions in math also don’t have side-effects, e.g. reading from file. But all these concerns are valid in the context of programming.

To summarise, here is a short list of possible things that functions in programming can do, and math functions cannot:

• Hang (loop indefinitely or takes unreasonable time to compute)
• Throw exceptions
• Terminate before producing a result in case of insufficient memory
• Have side-effects (read from files, send requests to web services, etc.)

Functional Programming is closer to the original math definition in the sense that its functions are pure – they have no side-effects. This essential FP paradigm allows us to talk about the concept of totality in a programming context, even though programming functions are very different from math functions.

Termination*🔗

advanced section, could be skipped

As we look at totality from the programming point of view, we need to describe a very close concept to totality — termination. Termination gives the guarantee that function does produce a result in a finite amount of time. Usually, when people talk about total functional programming, they mean programming with total functions that terminate successfully.

This concept of termination is more relevant to advanced languages called proof-assistants used to write proofs as programming functions. In such languages, successful proof must be a total and terminating function. Proof-assistants are invaluable in the software verification areas.

However, in real-life software, not all functions must be total. For instance, a Read-Eval-Print-Loop (REPL) or a Web Backend are not supposed to terminate eventually on their own. They should run infinitely and respond to requests in a timely manner.

The terminology of totality is a bit ambiguous in programming due to the different use-cases. In some places, total functions are required to terminate, while others require only to handle all inputs’ values. We will try to cover the most common definition of totality in this post.

Note as well that totality is not a straightforward and universally-applicable idea. We will make a few common simplifications in this post regarding totality in modern languages. But bear in mind that there are a lot of specifics that need to be kept in view. There are different methods of making functions total and guaranteeing this property for compiled vs interpreted, for typed vs untyped languages.

Another aspect — laziness; it also affects the work of pure functions in different ways. Infinite functions could be total (with termination notion) due to laziness. For instance, the following recursive function produces an infinite list. And if you’ll try to print the resulting list to the terminal, you will wait indefinitely for this function to finish:

multipliedByTwo :: Int -> [Int]
multipliedByTwo x = x : multipliedByTwo (x * 2)

However, due to laziness, you still can take the first five elements of the list and get the result:

ghci> take 5 (multipliedByTwo 3)
[3, 6, 12, 24, 48]

If being absolutely honest, Haskell is not a total functional programming language by default. It has a special value called “bottom” (⊥) that can be passed to any pure function. When such a value is being evaluated, it throws a runtime error. You can use standard Haskell functions undefined or error at the bottom. It means that even the pure and total function isZero we defined above could fail in runtime if used on bottom elements:

ghci> isZero undefined
*** Exception: Prelude.undefined
CallStack (from HasCallStack):
  error, called at libraries/base/GHC/Err.hs:79:14 in base:GHC.Err
  undefined, called at <interactive>:2:8 in interactive:Ghci1

ghci> isZero (error "I'm a banana, I do what I wanna")
*** Exception: I'm a banana, I do what I wanna
CallStack (from HasCallStack):
  error, called at <interactive>:3:9 in interactive:Ghci1

To design a complete total system, we need to have the input set without bottom (⊥) elements. An example of pure total language is Dhall — a configuration language where all functions must be pure, total and terminating.

If interested, you can read more about research in total functional programming (see in Links).

Not totally total🔗

Usually, in FP, you don’t use the phrase “total function” as, by default, functions are considered to be total. However, this can’t be the case all the time; it would be too easy. There is an opposite concept of totality – partiality, which means that a function is not defined for all inputs of its type.

Here are a few examples of common partial functions:

• Taking a list element by index. The index can be negative or be outside the list bounds, so it’s impossible to get the element in such cases.
• Parsing string to an integer. Not every string represents a valid numeric number, so a parsing function fails in such cases.
• Printf-like pretty-printing. If you specify the formatting with a separate string, it may fail at runtime on a wrong number of arguments or when types of arguments don’t match.
• Mathematical functions: division by zero, square root of a negative number, etc.
• Multiplication of matrices. If the dimensions of the two matrices are not aligned, it is impossible to multiply one matrix with another.
• Laziness brings more interesting partiality cases to the table. When you can have infinite lists, functions like sum, sort or reverse become partial because they hang on infinite lists.

Why should we care?🔗

As a developer, you have to deal with runtime exceptions all the time. Programming with total functions helps to avoid some of the runtime exceptions by ultimately preventing them from happening in the first place. But, at the same time, it requires time and discipline to write total functions. So you may think that writing total functions is a big price to pay for reducing the number of runtime exceptions since total functions won’t remove all exceptions entirely. But we believe that you actually should care about totality due to the few other perks as well:

• Even when writing a huge number of unit tests, you still can miss some cases. Total functional programming gives more guarantees about code correctness.
• Debugging runtime exceptions can be tedious for developers. But users of buggy products are frustrated even more. Spending more time on making functions total pays off in the long run.
• Total functional programming results in more maintainable, modular and composable programming. The composition of total functions is total. It means that you can refactor your code painlessly, split it into smaller and reusable parts, combine different components, and still be confident that it works. While working with partial functions, you may introduce new fragile logic not covered by tests, forget to update tests and experience unpleasant production failures.
• It is much easier to reason about total functions. You don’t need to keep track of all input states, whether they are valid and whether functions throw exceptions. Therefore, you can understand the existing code faster (and become more productive quicker as a consequence). Not to mention that code reviews will be more helpful and easier for everyone when you write and review total functions.

Partially correct🔗

We’ve already seen some examples of non-total functions above. But now, let’s take a closer look and focus more on recognising partiality and discussing different situations where it is possible to (unintentionally) introduce partiality. We will talk mostly about pure functions (except one example with IO for the sake of understandability) because this case is more interesting. Impure functions can easily be non-total due to exceptions.

👻Myth: all pure functions are safe

Even though pure functions don’t have side-effects and allow us to reason about the code easier, they still can be partial. So having purity is not enough for achieving maximal type-safety and guarantees from the compiler.

Few examples of the most dangerous places where to watch out for partiality:

Embedded pattern matching in function

Missing cases (non-empty list in this situation):

isEmpty :: [a] -> Bool
isEmpty [] = True

Case-of expression (similar to embedded pattern-matching)

Missing cases (the GT constructor of the Ordering type):

orderingToInt :: Ordering -> Int
orderingToInt ordering = case ordering of
    LT -> -1
    EQ -> 0

Guards

Uncovered conditions unders the guards:

orderingNumber :: Ord a => a -> a -> Int
orderingNumber x y
    | x < y = -1
    | x == y = 0
    | x > y = 1

In this case, if using this function on Doubles, we can get to the point where none of the conditions will apply (e.g. with NaN). In this case, it is good to have a terminal check.

Pattern-matching in lambdas

Though this is very handy to write functions quickly, it is not an easy to write all-encompassing pattern matching with lambda:

takeHeads :: [[a]] -> [a]
takeHeads = map (\(x : _) -> x)

Usually, lambdas are used with the (named) wildcard patterns instead.

Pattern-matching in let-in

Similar to the case with lambdas pattern matching, you can bump into a similar behaviour:

let Just myVal = Map.lookup myKey myMap

Pattern-matching in where

patchParagraph :: [Text] -> [Text]
patchParagraph paragraph = ...
  where
    title : _ = paragraph

Pattern-matching in binds: <-

main :: IO
main = do
    [inputFile] <- getArgs

Note: watch out for MonadFail instances; sometimes, it can be reasonable to do so.

Unspecified fields of record data types during initialisation

data User = User
    { userName :: Text
    , userAge :: Int
    }

newUser :: User
newUser = User { userName = "New User" }

Note: this is valid because Haskell is lazy, and all unspecified fields are initialised with error.

Records inside sum types

data Address
    = Address { street :: Text, country :: Text }
    | NoAddress

When using records inside sum types, you get partial getters (street and country) and partial record-update syntax.

Error

Using “bottom” function error:

zipEqual :: [a] -> [a] -> [(a, a)]
zipEqual [] [] = []
zipEqual (x:xs) (y:ys) = (x, y) : zipEqual xs ys
zipEqual _ _ = error "Expecting lists of equal size!"

Undefined

The special case of error without a custom error message:

hash256 :: Text -> ByteString
hash256 = undefined

Non-terminating unintentional loops

increment :: Int -> Int
increment x = let x = x + 1 in x

Partial primitive functions

ghci> naturalFromInteger (-3)
*** Exception: arithmetic underflow

Type class instances (non initialised, standard type classes giving errors)

data State = Open | Closed

instance Eq State

Compiler panics

Sometimes our compilers have bugs or low-level panics in their core functions. It results in having partial functions in applications.

stan: stan: panic! (the 'impossible' happened)
  (GHC version 8.8.3 for x86_64-unknown-linux):
    readHieFile: hie file versions don't match for file: .hie/Relude.hie Expected 8083 but got 8082

Please report this as a GHC bug:  https://www.haskell.org/ghc/reportabug

Segmentation fault

Even more low-level errors, usually on the level of operating with memory or Operating System interface manually.

Fake totality🔗

As in many other areas, people sometimes prefer “fake” safety to no safety at all. So just as a box-ticking exercise, we plug partiality with seeming safe case checking. Even if the function becomes total, there could be a few additional problems with such shaky solutions.

Let’s look at a few examples of such tricks.

Wildcards🔗

Pattern matching, as we’ve seen, is a frequent candidate for leaking partiality. And the go-to solution for many cases is to use a wildcard – the pattern that fits anything. It leads to having a case that will fire up anyway if none of the above patterns worked.

data Status
    = Approved
    | Rejected

run :: Status -> Result
run s = case s of
    Approved -> runApprovedAction
    _ -> runRejectedAction

However, it could affect you in the future if you, for example, tweaked the type a bit to add another status.

data Status
    = Approved
    | Rejected
    | Cancelled

The problem is that the function still covers all cases of Status, but it doesn’t do the right thing on the newly added status. In other words, the function is total but is still incorrect. In the case of using wildcards, you should be very careful not to forget any of such places, as even the compiler won’t help you with that, as this is a totally fine function!

To avoid such situations, you can use pattern matching on every pattern without using wildcards when possible.

Promises we give🔗

Sometimes we are sure that some event can’t possibly happen. And it may be an absolute truth, but the compiler is not convinced. And rather than trying to be more accommodating with that, we sometimes catch ourselves writing something like:

error "impossible happened, lol"
error "never ever going to happen, I promise"

Then we roll our eyes seeing something like this while running our app:

*** Exception: never ever going to happen, I promise
CallStack (from HasCallStack):
  error, called at <interactive>:3:5

The problem with this is that it is not adjustable to logic changes. With such promises you give, you state a lot of logic in one line. However, not all entries of usage of your functions could guarantee that they are aware of this agreement.

Name convincing🔗

Another technique we tend to use from time to time is safety-by-naming. When you are sure that the function can accept only a particular input and that no other input could be provided to the function from anywhere, you can indicate that using type synonyms (the simple new name for the type).

type NonNegative = Int

lastDigit :: NonNegative -> NonNegative
lastDigit n = n `div` 10

However, nothing would stop to use the lastDigit function with negative numbers:

> lastDigit (-25)
-3

The purpose of NonNegative type name was in self-documentation. And it works if this function is internal and guaranteed to be used only in specific places; however, this is tricky to control in big codebases.

Trust🔗

Do not trust every pure function from other libraries. Yes, this is correct that partial functions should be highlighted in the documentation, though, sadly, it is not always true. And this can come from anywhere! For example, the standard library in Haskell. People could falsely assume that the most essential and primary library in the language is trustworthy, but watch out! base (name of the standard library) provides a number of partial functions, so you need to know about that to be able to get around that.

For example, the maximum function from the base, that returns the maximum value from the provided list of elements, fails in the runtime if the list is empty:

maxOfTwo :: [Int] -> [Int] -> Int
maxOfTwo list1 list2 = max (maximum list1) (maximum list2)

The moral of this point is not to question every other thing that is not written for you. The advice here is to keep an eye on commonly-known precedents and try to be in the know.

Totality fighters🔗

Now that we know a few common non-total patterns that can be met in codebases, let’s look at the most popular and effective ways to achieve totality.

General🔗

This section will show some of the common solutions. However, all of the solutions can bring additional burden to the way you would organise your code later, so use wisely and consider trade-offs.

Returning the default value🔗

In many cases, partiality comes from the impossibility to return anything as a result. For instance, when you want to get the first element from the list, we couldn’t return anything meaningful when the list is empty. In some of those cases, we can use some default value established in the right way.

For example, we can extend the partial function to take an argument that we can use as a result when something went wrong. However, there is a way to do it without adding any new arguments. The Monoid typeclass contains inside the “default” or “initial” value of the data type with an instance of Monoid. It is called mempty. It is useful because it could be used as the returning value if the result could be found in another way.

Returning maybe/either/validation🔗

The previous point methods won’t work on some types, where we can not decide on the “default” element (what is the default for integers? Is it 0 or 1 or -1?). This is where optional results are useful. Instead of saying that the function will definitely return you a value, we would say that it will maybe return a value or maybe not.

For representing such data, in Haskell, there are several such optional sum types that represent “Or” situation:

• Maybe a – represent Just a value or Nothing at all.
• Either e a – similar to Maybe but allows to put more context into the Nothing case.
• Validation e a – similar to Either but allows you to accumulate all kinds of failing cases in one go when you want to combine multiple Validations later.
• These a b – Allows having one of, two or none results at the same time.

This technique is so popular that some alternative standard libraries in Haskell have chosen this approach to neutralise partial functions present in the base library.

Restrict input types🔗

An alternative to patching output types to represent what the function can return to us more accurately, we can think of improving the types that our function can take.

For example, when we want to take the first element of the list, we are pretty sure that there is at least one element. So why not specify that in the input itself? We can narrow down what the function can take and have lots of benefits from this. The NonEmpty list data type denotes that the list always has at least one element.

nonEmptyHead :: NonEmpty a -> a

Separate specialised functions instead of common typeclasses🔗

Another problematic point is when we state that some data types can do more than they actually can. This could peep out, for example, in some typeclass instances. When you define an instance of some typeclass, you must implement all methods of this typeclass. But in some cases, it is not possible.

One example of such a typeclass is Num and its instance for the Natural type. Natural doesn’t have negative numbers, but Num contains methods of negating and subtracting values, leading to partial functions throwing errors in runtime.

The solution in such cases would be to create smaller abstractions towards bigger ones that would contain more power. Specifically here, Num could be separated into a few typeclasses: one of them shouldn’t have negation, so this would be convenient to use Int and Nat together and not worry about getting a runtime exception depending on the type you use.

On the other hand, if you see that your data type doesn’t really fit some of the existing abstractions, it might be right not to provide an instance of such a typeclass, even if it leads to a less convenient API.

Haskell-specific🔗

Haskell provides several tools for reducing partiality in your code. There could be similar instruments in other functional languages, so we will try to describe the concept of them applicable to Haskell in this particular case.

Compiler🔗

The first and the most important instrument that will help you fight partiality is the compiler itself. In Haskell it is Glasgow Haskell Compiler (GHC). GHC provides several warnings and sanity-checks that are particularly useful for totality checking. For instance, checks on non-exhaustive pattern matching or uninitialised records.

However, be aware that those warnings are not enabled by default. And we strongly recommend compiling your Haskell projects with the following flags:

• -Wall — this flag includes multiple useful warnings, and specifically in the area of totality, tells GHC to check for non-exhaustive pattern-matching

• -Wincomplete-uni-patterns — enables pattern-matching coverage checker for internal variables and lambdas

• -Wincomplete-record-updates — warns when the record-update syntax is used with data types that contain records inside sum types.

• -Wpartial-fields — warns when defining a sum type with a partial record field inside.

  The easiest way to enable them universally is to add to a common stanza so that it would be applied to all parts of your project at once.

Static Analyser🔗

In addition to the compiler effort, you can use static analysers to help you more with totality. In Haskell, there is the Stan analyser; it warns you on the usage of commonly-known partial functions that fail due to non-exhaustive pattern-matching or hang when given infinite lists as inputs. Moreover, it helps with some fake-totality cases, such as usages of undefined or wildcards in pattern matching on sum types (like in the example from the “Fake totality” section).

Program Verification Tools🔗

As another option of totality/termination guarantees, you can utilise a verification tool. Haskell has LiquidHaskell – an instrument to enforce critical properties at compile time. When using this tool, you can write additional annotations to your functions in the code specifying requirements for inputs, and LiquidHaskell will check them if you run it. LiquidHaskell has a specific goal to eliminate partiality and non-terminating functions.

Because Haskell is pure, the only effects it allows are divergence and incomplete patterns. If we rule out both these effects, using termination and totality checking, the user can rest assured that their functions are total, and thus correctly encode mathematical proofs. Unfortunately, creative use of certain features of Haskell, in particular data types with non-negative recursion and higher-rank types, can be used to write non-terminating functions that pass Liquid Haskell’s current checks. Until this is fixed, users need to be careful when using such features.

Future🔗

Languages with Dependent Types (DT), such as Idris, Agda or Coq, can boast having eliminated a whole layer of partial errors. DT allows you to make your values dependable on other types and patterns you are working with at the moment and also use them as first-class objects (pass to functions).

All examples of partial functions we’ve given before (matrix dimensions, printf, division by zero, getting element by index) can be converted to total with the help of DT. You will need to specify your requirements as additional constraints in type signatures, like on the examples below:

div :: (x : Int) -> (y : Int, y /= 0) -> Int

elementAt :: (xs : List a) -> (i : IntNoBiggerThan (length xs)) -> a

Would DT solve all of the totality issues? Maybe. But it depends.

We see that most of the dependent type systems were architected with the totality in mind. See the following quote on the importance of totality:

Totality is important for dependently typed programs, partly because non-terminating proofs are not very useful, and partly for reasons of efficiency: if a certain type has at most one total value, then total code of that type does not need to be run at all.

So hard🔗

While reading this blog post, you may think that achieving totality is hard. And it indeed looks like a lot of things to keep in mind, as well as following some discipline:

• Use pure functions when possible
• Check for all patterns when performing pattern-matching
• Enable proper compiler warnings
• Use external static analysers or program verifiers

All these steps touch different parts of the workflow and require interacting with various components. Not everything can be automated. Some steps require thorough thinking about the architecture (e.g. thinking about modelling your problem with immutable data and pure functions instead of mutable references and IO). So automating all of them is not always straightforward. But it pays off eventually to invest in totality for your code.

It’s worth mentioning that even basic totality-checking constructs, such as patterns coverage checks, are not always easy to implement in tools. For instance, the following function is total, even though each individual patterns are not total on their own.

ordSub :: Ordering -> Int -> Int -> Int
ordSub ord x y = case ord of
   EQ -> 0
   _ -> case ord of
       GT -> x - y
       LT -> y - x

But for a long time, GHC wasn’t able to tell that. However, the latest release of GHC, the 9.0 version, can verify that this function is indeed total.

You can see how totality checking can be challenging to implement even for fundamental parts of Functional Programming. But it would help every one of us a lot if more automated totality tools were acceptable to users by default. Until then, it is a noble and right thing to use what we have now: enable compiler options, configure and use tools (especially on CI) to detect partiality, and use established techniques and best-practices in libraries to provide total code.

Conclusion🔗

Even being the core concept of Functional Programming, Totality is something that you need to work on in order to get that. It is not coming for free. You do not have any guarantees that you won’t have runtime exceptions in pure functions if you write in some particular FP language. There are lots of ways to shoot yourself in the foot. But it is crucial to understand what totality does, how it serves us and be able to identify partiality when you see it.

Links🔗

• Wikipedia: Total Functional Programming

• Wikipedia: Partial Function

• Total and partial functions in FP

• Total function & partial function: Definition

• What is a total function?

• SO: What are total and partial functions?

• Total functional programming

• “Total functional programming” by D.A.Turner

• LiquidHaskell: Totality Check

• Totality and Termination

• ΠΣ: Dependent Types without the Sugar

• SO: What is Haskell missing for totality checking?

• “Making Impossible States Impossible” by Richard Feldman

Credits🔗

Many of this blog post’s illustrations were inspired by the Mortal Kombat game. Specifically, we used some of the images and gifs from the game, and some of the elements are adapted to similar situations from the game.